Package org.jcurl.math

Generic math helpers without dependencies to other jcurl packages.

See:
Description

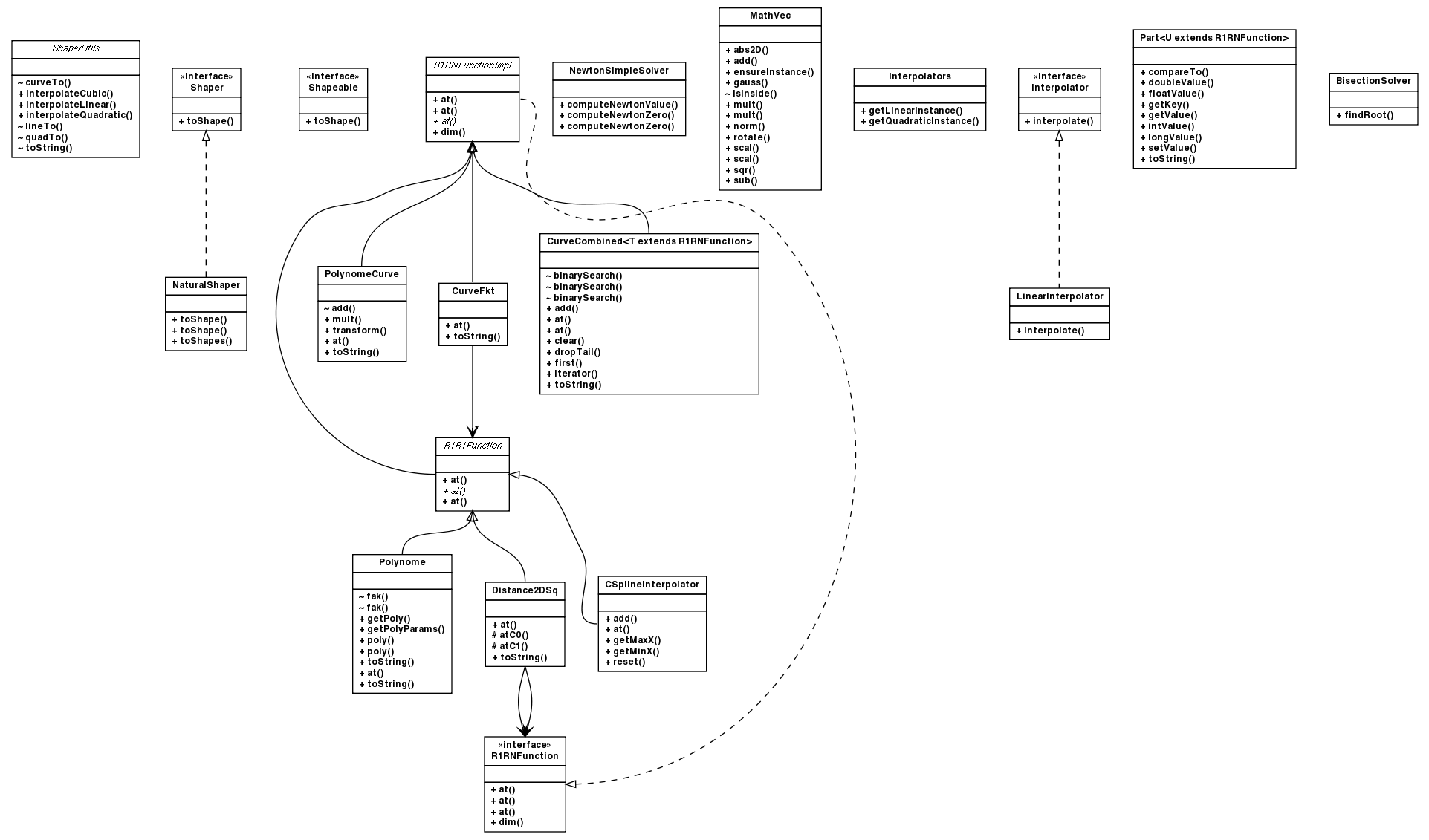
Interface Summary

Interpolator	Re-implementation of Scenario Interpolator.
R1RNFunction	Interface for n-dimensional curves f : R^1 -> R^n.
Shapeable	Indicate that the class may support a native Shapeable.toShape(double, double) method.
Shaper	Turn a R1RNFunction into a Shape.

Class Summary

BisectionSolver	Bisection root-finding algorithm.
CSplineInterpolator	The numerical algorithms are adapted from "Meyberg/Vachenauer": Hoehere Mathematik I, second edition.
CurveCombined<T extends R1RNFunction>	Combined curve.
CurveCombined.Part<U extends R1RNFunction>	One segment of the combined curve.
CurveFkt	A n-dimensional, continuous curve R -> R^n based on R1R1Functions.
Distance2DSq	The distance between two R1RNFunctions - only 2 dimensions used.
Interpolators	Provides a number of built-in implementations of the Interpolators.LinearInterpolator interface.
Interpolators.LinearInterpolator
MathVec	Helper class that brings some (2D-)vector artihmetics.
NaturalShaper	Use Shapeable.toShape(double, double) only.
NewtonSimpleSolver	Very simple implementation of Newton's root-finding algorithm.
Polynome	Polynomes of n-th grade.
PolynomeCurve	Multidimensional curves of polynomes.
R1R1Function	A one-dimensional function f : R^1 -> R^1.
R1RNFunctionImpl	Abstract base class for n-dimensional curves f : R^1 -> R^n.
ShaperUtils	Helper for convenient approximated Java2D drawing of arbitratry R1RNFunctions with at least 2 dimensions.

Package org.jcurl.math Description

Generic math helpers without dependencies to other jcurl packages. Could even be a separate binary - therefore it's package name is not org.jcurl.core.math

Why isn't math library X used?

First of all every library is likely to bring unneeded/unwanted stuff but this core library should remain slim and fast, concerning both download and runtime. It should be useable within applets or java webstart over slow networks. Therefore it also has to have as few dependencies as possible.

Second the requirements here are rather simple. R^1 -> R^3 monotone, C1 continuous functions. That's all.

Third I use a dirty trick to pack up spatial (2D) and angular position and speed into one 3D Rock. This contradicts the JSR-275 measure concept, so jscience will not like this.

But nevertheless the following libs were examined:

Jakarta Commons Math

• brings quite a bit unneeded stuff (jar of 331K),
• Exceptions on function evaluation,
• getting derivatives seems a bit a hassle (via the regular Interfaces),
• No interfaces for multi-dimensional functions

JScience

• brings a lot of unneeded stuff (jar of 680K),
• heavy Boxing/Unboxing because of generics (maybe this isn't critical?),
• evaluating a function seems to change inner state and therefore might not be threadsafe.
• type-checked measures require derivatives to be different classes (at least with a different type parameter)

I admit that jscience is really tempting. I'll keep an eye on it.